forum.farmanager.com
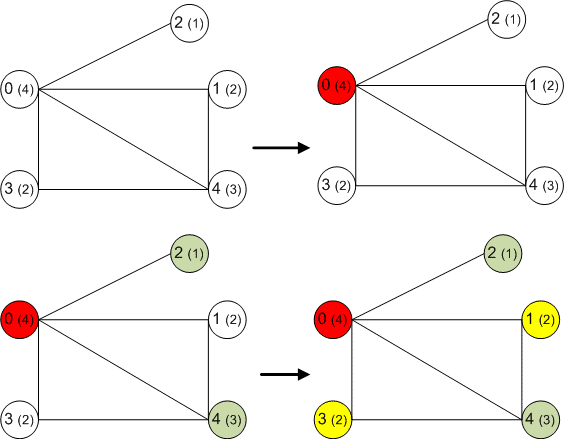
Существует много эвристических процедур раскрашивания графов, позволяющих находить хорошие приближения для хроматического числа графа в тех случаях, когда размеры графа слишком велики и получение оптимальной раскраски точными методами затруднительно. Здесь дается краткое описание одной из таких процедур и ряда ее разновидностей. В этом простейшем из методов вершины вначале располагаются в порядке невозрастания их степеней. Первая вершина окрашивается в цвет 1; затем список вершин просматривается сверху вниз по невозрастанию степеней и в цвет 1 окрашивается всякая вершина, которая не смежна с другой, уже окрашенной в этот цвет.









Customer Reviews, including Product Star Ratings help customers to learn more about the product and decide whether it is the right product for them. Instead, our system considers things like how recent a review is and if the reviewer bought the item on Amazon. It also analyzed reviews to verify trustworthiness.











Is data on this page outdated, violates copyrights or anything else? Report the problem now and we will take corresponding actions after reviewing your request. Publication date 1 January Abstract В дискретной математике известны разные алгоритмы раскраски графов: точные, переборные, эвристические.