Графы: представления, достижимость и связность
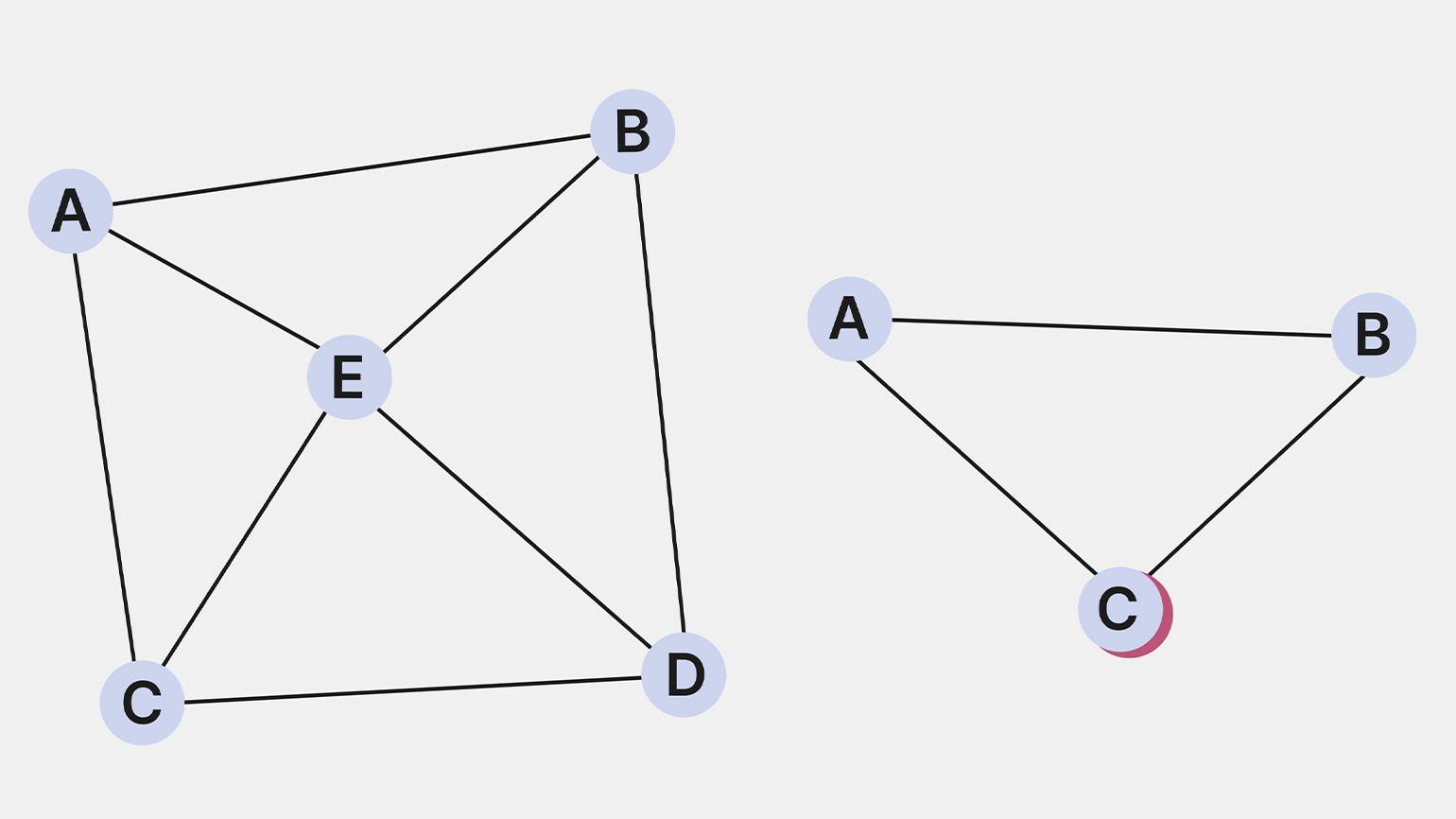
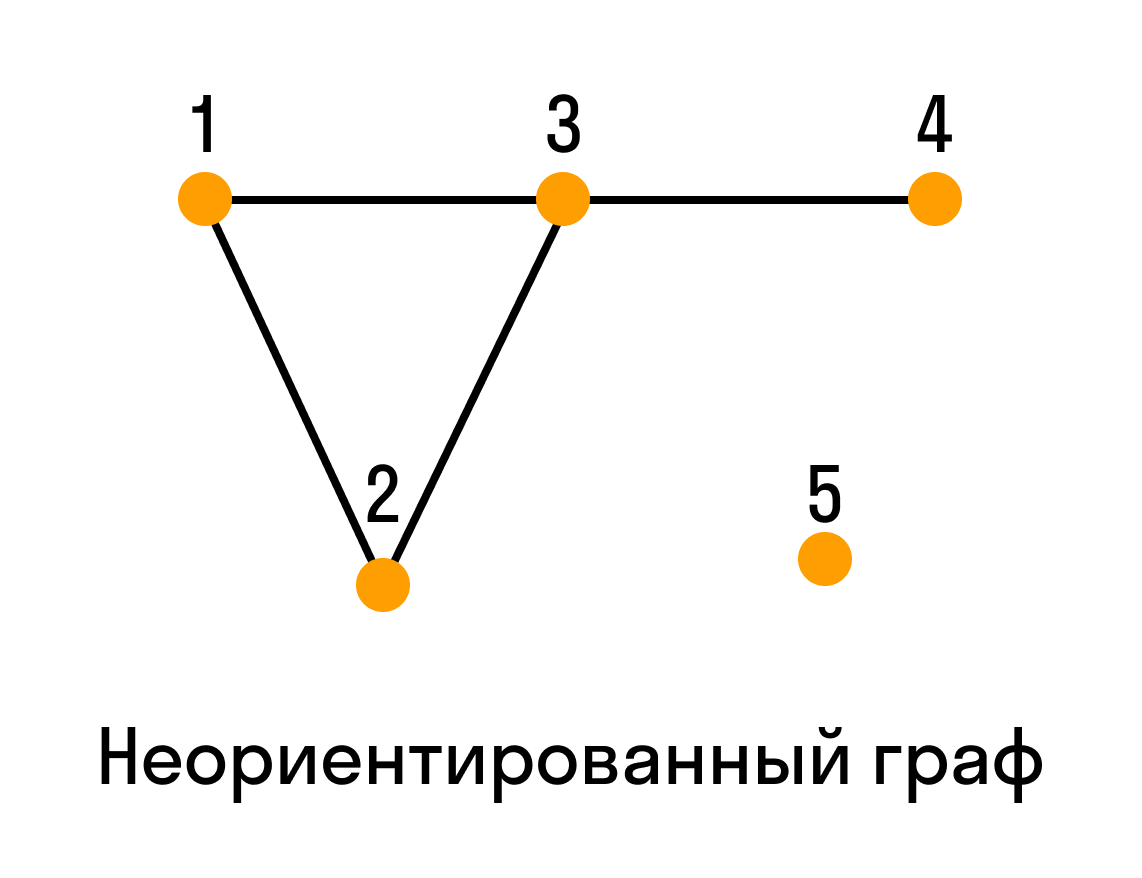
Материал из Викиконспекты. Перейти к: навигация , поиск. Дополнительный граф к несвязному графу связен. Категории : Алгоритмы и структуры данных Основные определения теории графов. Навигация Персональные инструменты Создать учётную запись Войти.



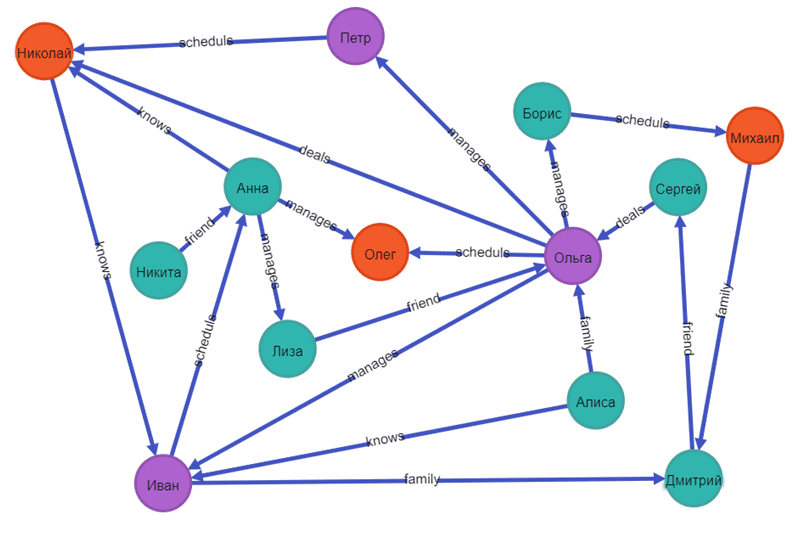


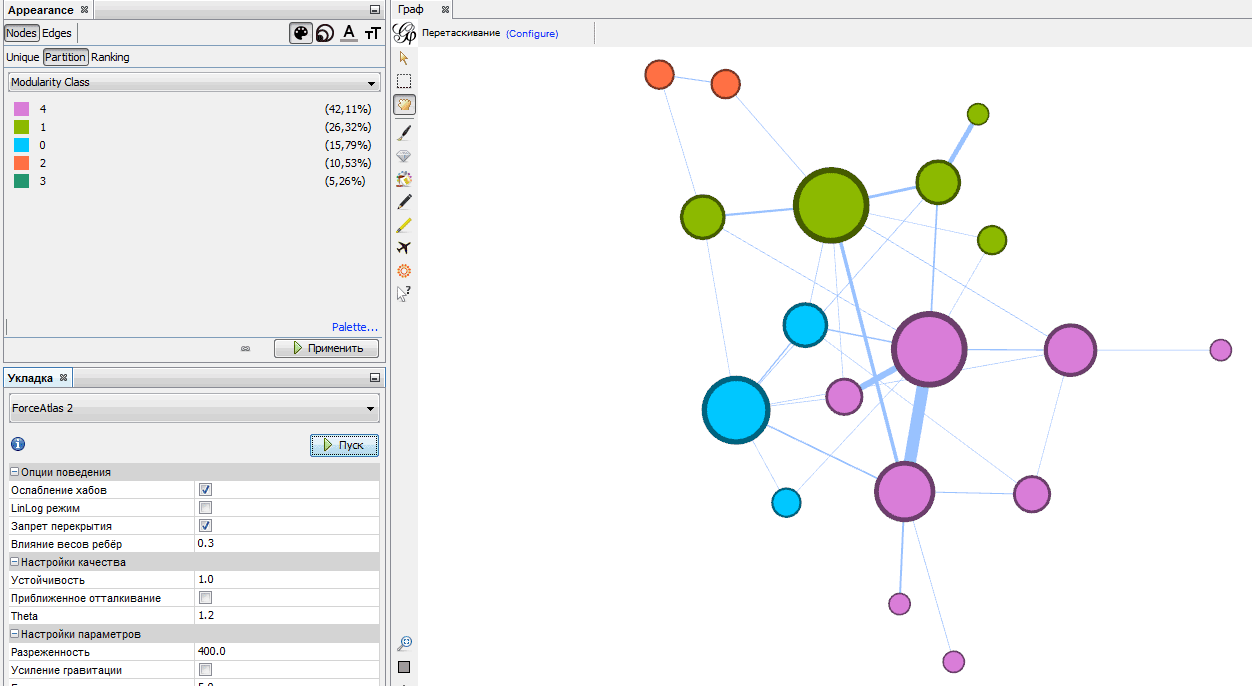
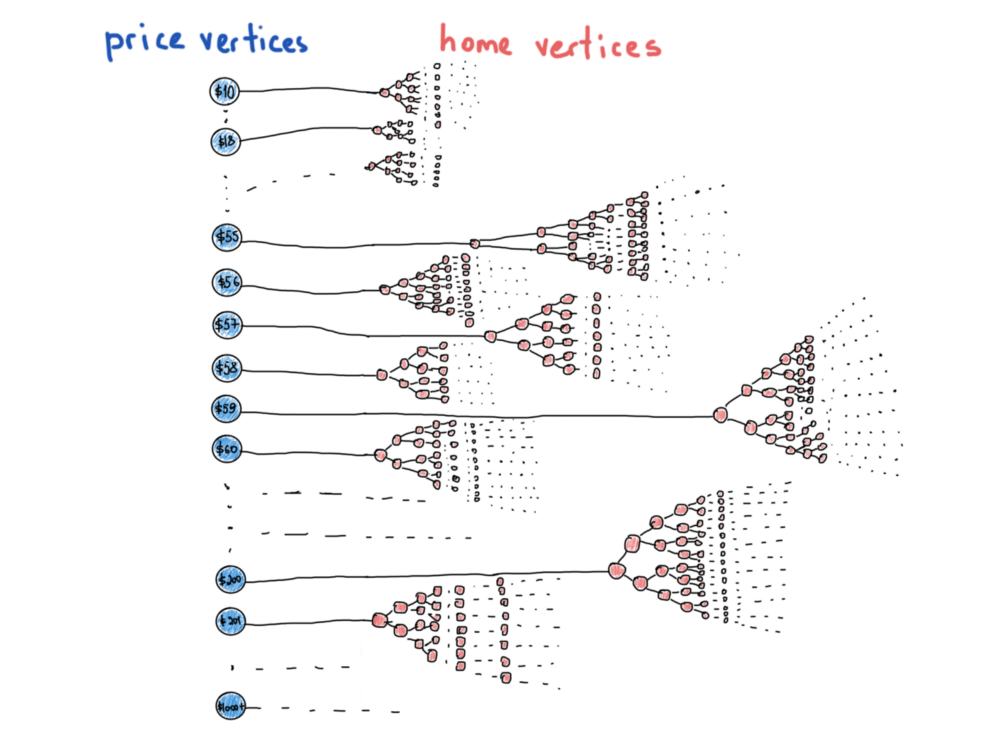
Поиск Написать публикацию. Время на прочтение 7 мин. Ранее мы публиковали пост , где с помощью графов проводили анализ сообществ в Точках кипения из разных городов России.


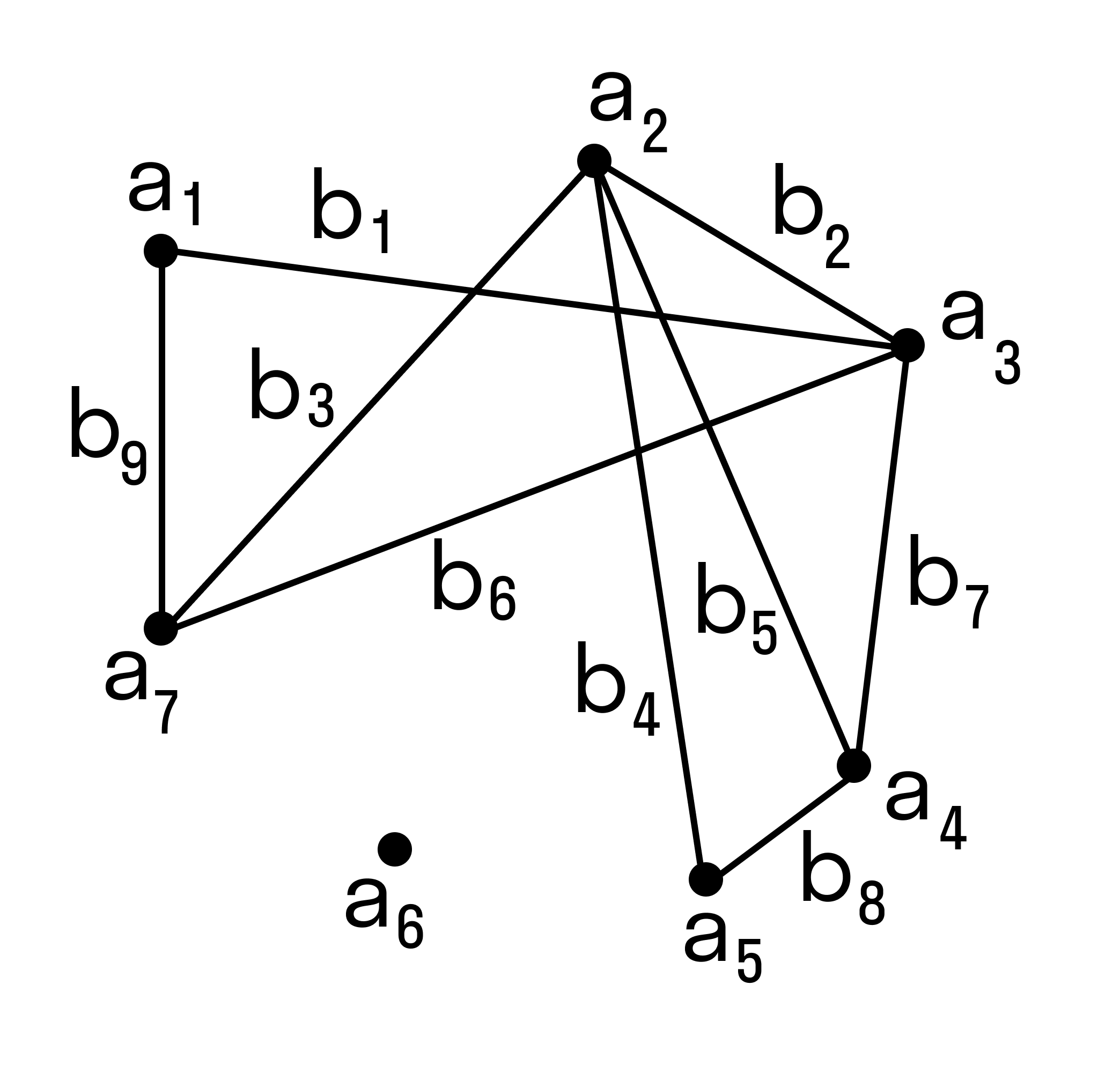

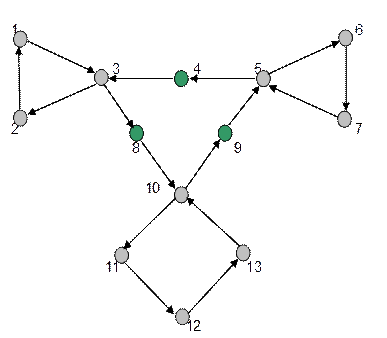
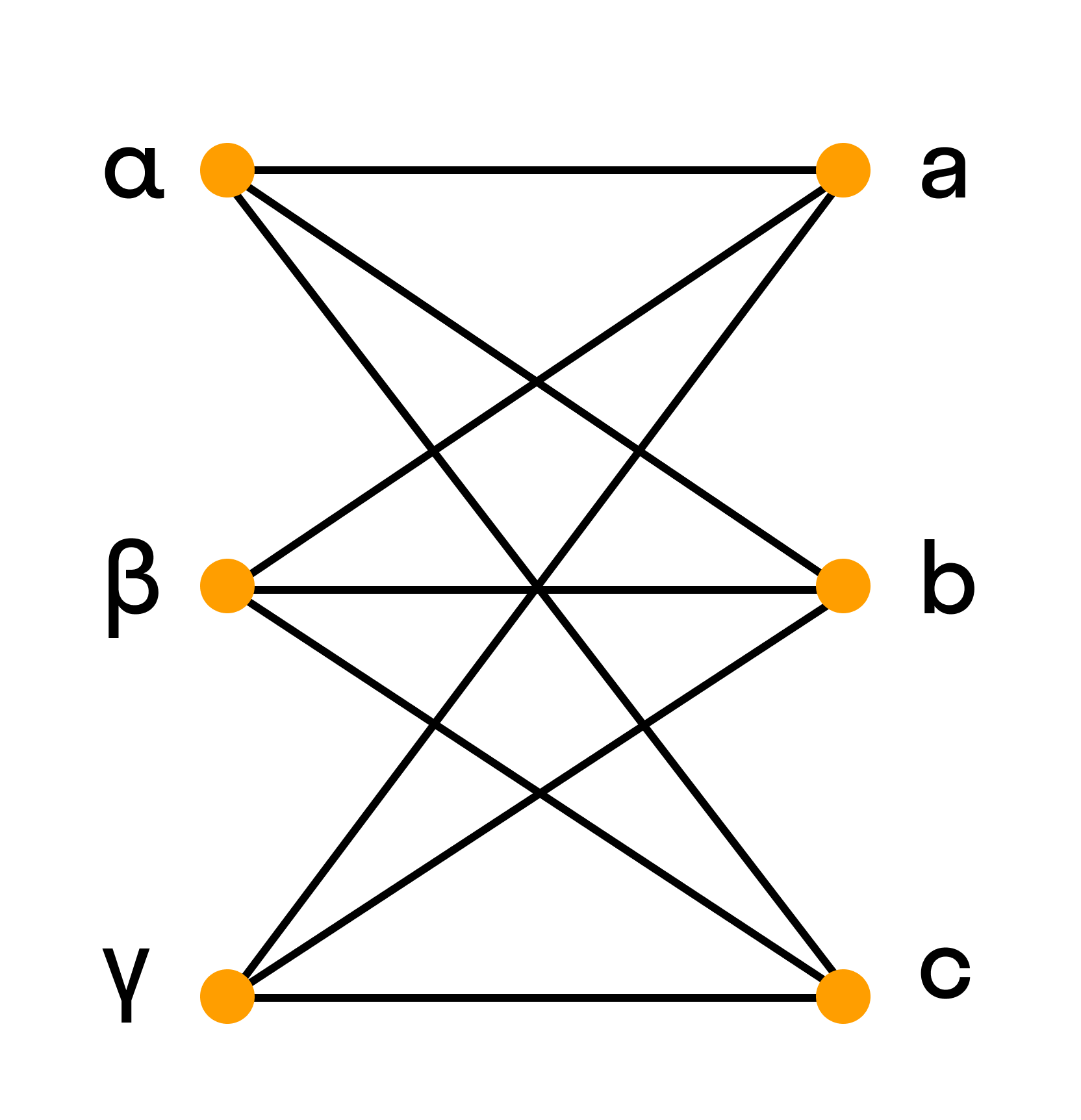
В теории графов рёберным графом L G неориентированного графа G называется граф L G , представляющий соседство рёбер графа G. Понятие рёберного графа для данного графа настолько естественно, что независимо было введено многими авторами. Конечно, каждый из них давал своё название: Оре [ 1 ] назвал этот граф «смежностным графом» , Сабидусси [ 2 ] — «графом производной» , Байнеке [ 3 ] — «производным графом» , Сешу и Рид [ 4 ] — «рёберно-вершинно-двойственным» , Кастелейн [ 5 ] — «покрывающим графом» , Менон [ 6 ] — «присоединённым» «сопряжённым» [ 7 ] [ 8 ] [ 9 ]. Одна из наиболее ранних и наиболее важных теорем о рёберных графах принадлежит Уитни, который доказал, что, за одним исключением, структура графа G полностью определяется рёберным графом.